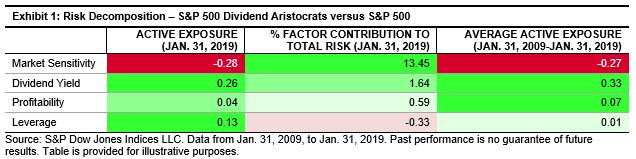
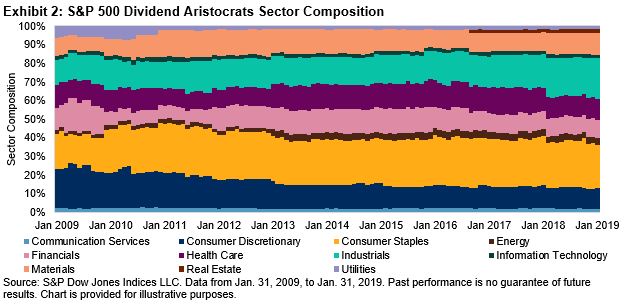
Our SPIVA® readers often ask what percentage of outperforming funds goes on to beat the market over the following years. Our latest research report, Fleeting Alpha: The Challenge of Consistent Outperformance, answers that exact question in detail.
In this blog, we demonstrate the difficulty and likelihood of consistently outperforming a benchmark.
Using trailing three-year returns from Sept. 30, 2012 to Sept. 30, 2015, we found that 298 large-cap funds (27.38%), 123 mid-cap funds (29.55%), and 101 small-cap funds (16.64%) outperformed the S&P 500®, the S&P MidCap 400®, and S&P SmallCap 600®, respectively.
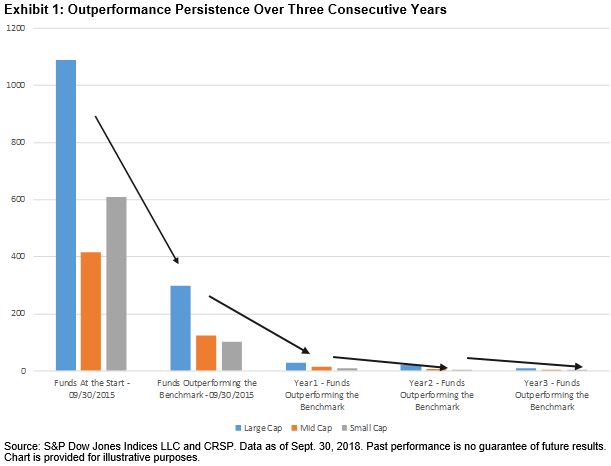
The following year, based on one-year returns as of Sept. 30, 2016, only 9.38% of large-cap managers, 11.54% of mid-cap managers, and 7.78% of small-cap winners beat the benchmarks. By the end of September 2018, only 2.73% of the 298 winners were able to maintain that status for three consecutive years. Exhibit 1 shows the decline in the percentage of managers who were able to outperform the markets continually.
Because cyclical market conditions can unduly influence a point-in-time snapshot like the analysis above, we also performed the same exercise on a rolling quarterly basis from March 31, 2003, to Sept. 30, 2018, and averaged the figures. This resulted in a smoother trend line that is more indicative of the long-term performance persistence (see Exhibit 2).
On average, there was a fair degree of outperformance persistence in the first year across most categories. However, we see an inverse relationship between the level of persistence and the time horizon; persistence declined in each subsequent year.

Over the long term, roughly 24%-26% of large-cap, mid-cap, and small-cap managers outperformed their benchmarks in a given year. Approximately 30%-33% of these managers went on to outperform again in the next year. There was a similar dramatic decline in the percentage from year 2 to year 3. From one year to the next, only about a third were able to beat the market again.
The probability of beating a benchmark for three consecutive years was only 2.4%-3.7%. Out of all the actively managed funds available in the U.S. (1,765 on average), only 30 large-cap managers, 10 mid-cap managers, and 20 small-cap managers possessed this rare skill. Market participants may want to reconsider chasing “hot hands” or picking managers based on past performance.
The posts on this blog are opinions, not advice. Please read our Disclaimers.