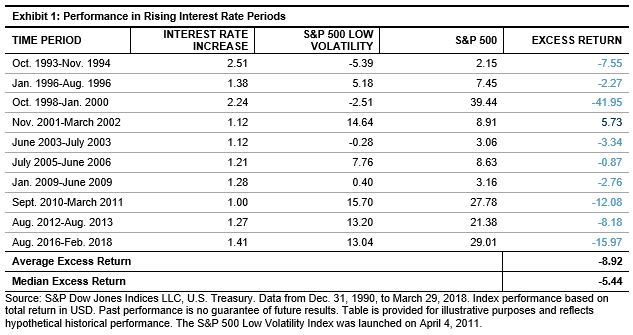
In a previous blog, we performed preliminary exploration of rising interest rate exposure of the S&P 500® Low Volatility Index. In this blog, we continue the analysis to see if there is a relationship between the magnitude of interest rate change and magnitude of active return of the low volatility index relative to the S&P 500. To do so, we run a regression line by plotting the historical monthly excess returns (y-axis) against the monthly interest rate changes (x-axis).

Looking at the trend line in Exhibit 1, there is a downward sloping, negative relationship between the degree of interest rate movements and the excess return of the low volatility index relative to the S&P 500. The regression equation, also shown in the chart, confirms the negative relationship.
The regression equation has a slope coefficient of -3.07 and an r-squared value of 8.8%. The coefficient indicates that for every 1% change in interest rate, the excess return of the low volatility index is expected to change by -3.07 times. For example, if interest rates rise by 1%, the relative return is expected to be -3.07%. Conversely, if rates decline by 1%, the excess return is expected to be 3.07%.
The r-squared value is the trend line’s “goodness of fit” to the data; in essence, it is the explanatory power of interest rate movements on excess returns. We note that the r-squared value is relatively low; however, the coefficient to interest rates is statistically significant. Ensuring that coefficients are statistically significant when it comes to factors that have low explanatory power, such as macroeconomic factors, on equity performance is especially critical. In this case, the t-stat of the interest rate change coefficient is -5.61, which is significant at the 99th percent confidence interval.
Combined with the findings in the first blog, we can conclude that, historically, the S&P 500 Low Volatility Index tends to be negatively affected by rising interest rates. In a subsequent blog, we will explore an alternative low volatility index strategy that is designed to reduce interest rate exposure while still preserving low volatility properties.
The posts on this blog are opinions, not advice. Please read our Disclaimers.