After last week’s FOMC meeting, the time when interest rates begin a sustained rise propelled by the Federal Reserve may be drawing closer. The received wisdom is that no one should own bonds when interest rates are rising because rising rates mean falling bond prices. While the math demands that bond prices fall, a deeper look at the math reveals that all may not be lost.
Some investors believe that the yield to maturity on a bond measures the return they will earn if they hold the bond until it matures. Not quite. There is a hidden assumption that the coupon payments received every six months will be reinvested and will earn the same rate as the yield to maturity. Since interest rates can vary over time and different rates are available for different time frames, this assumption rarely holds. When interest rates climb after a bond is issued, the price of the bond drops but the returns earned from reinvesting the coupon income benefits from the higher interest rates. (The reverse also holds, if rates fall after the bond is issued, its price rises but the returns or “interest on interest” from reinvesting the coupons is less.) If you buy a bond and interest rise far enough and fast enough, you might do better than if rates never moved at all.
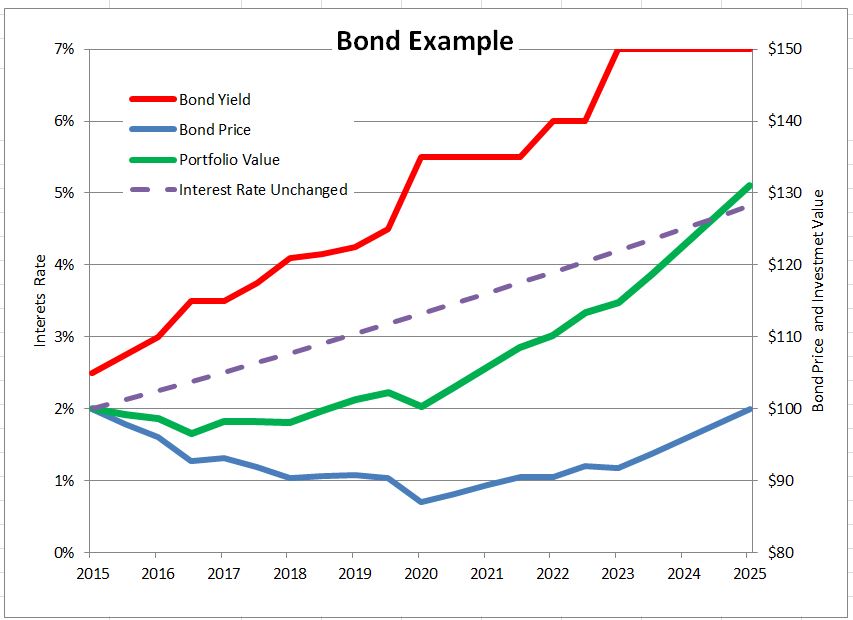
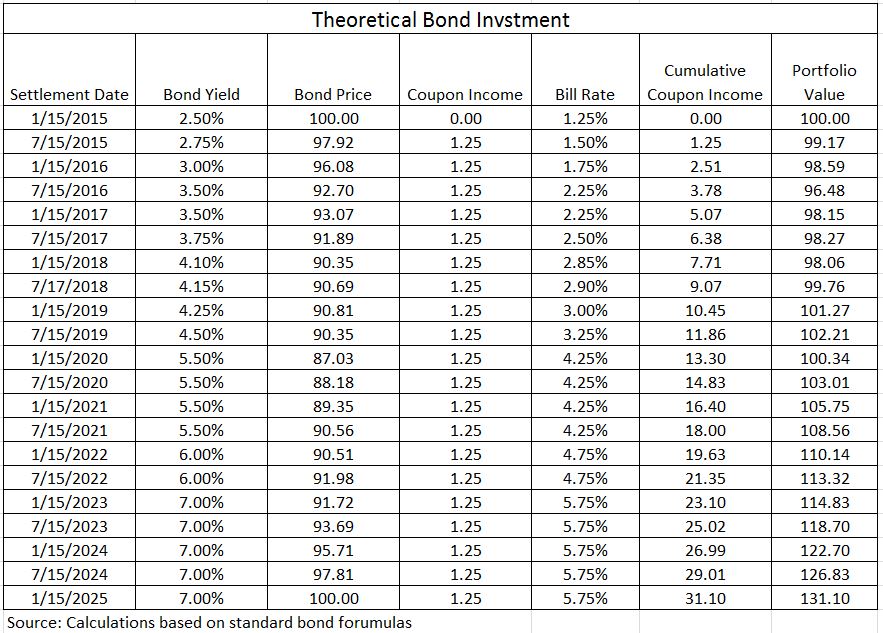
A made-up example shows how this might work and how the investor who holds the bond long enough could benefit. The table shows a theoretical investment in a 2.5% coupon ten year Treasury note bought on January 15, 2015 at a price of 100. The yield to maturity when purchased is 2.5%. If rates don’t change and if each semi-annual coupon payment of $1.25 can be invested at 2.5% annual rate for the remaining life of the bond, the investment will be worth $128.20 on January 15, 2025 when the bond matures. The dashed purple line on the graph illustrates this; the right hand scale is the value of the investment in the bond and the coupons.
Now let’s change the example shown on the table – interest rates rise and the yield paid on newly issued treasury notes rises towards 7% as shown in the second column of the table. Further, the coupon income is reinvested in six-month T-bills which pay 1.25% less than treasury notes. The table works out this example: every six months a coupon payment is received and it is added to the past coupon income and the total is invested at the T-bill rate. These coupon payments – the interest paid on the bond – earn “interest on interest.” At the end of ten years the accumulated coupons total $31.10 ($25 of payments plus $6.10 interests earned on the coupons). The total investment is worth $131.10. The green line on the chart plots the investment value. In the early years the rising rates depress the bond price and send the investment into negative territory. As the accumulated coupon interest increases and as the bond approaches maturity, the investment moves into positive territory and surpasses the theoretical case of no change in interest rates (the dotted line).
If it is possible to make money with bonds when interest rates rise, why are so many people worried that rates will rise? The blue line at the bottom of the chart plots the price of the bond for the same time pattern of rising interest rates. Just as the math requires, rising rates mean lower bond prices. At maturity approaches the price approaches the par value of the bond – the principal to be repaid at maturity. If an investor didn’t reinvest the coupons, if instead he spent the coupon income, all he would have at maturity is the par value. Likewise, if the investor had sold out at the low point on the green line (July 15, 2016) the proceeds for the $100 invested would have been $96.50, a loss of $3.50.
There are no magic formulas for bond investing in any interest rate environment, but working the math sometimes helps.
The posts on this blog are opinions, not advice. Please read our Disclaimers.